Lab 9
Bubble Chamber Pictures
and
the Identification
of Particles
Bill Chun Wai Hung
Marjan Montakhab
Nimish Kumar
Friday Section
Data
and Calculation:
Table 1.
|
Elements |
h (cm) |
l (cm) |
r (cm) |
mv (MeV/c) |
E(MeV) |
|
Pi- |
5.7 |
30.6 |
84.9868421 |
764.881579 |
777.588471 |
|
Alpha |
5 |
31.7 |
102.989 |
926.901 |
(Table 2) |
|
Beta |
4.4 |
17.5 |
37.0011364 |
333.010227 |
(Table 2) |
Table 2.
|
Elements |
Rest Energy (MeV) |
Total Energy(MeV) |
|
p |
938 |
1318.7 |
|
pi+ |
140 |
937.4 |
|
k+ |
450 |
1030.4 |
|
pi- |
140 |
361.2 |
|
k- |
450 |
559.8 |
Table 3.
Known Energy Values
|
E(pi-)(MeV) |
E(p)(MeV) |
E(pi-)+E(p)(MeV) |
|
777.588471 |
938 |
1715.588471 |
Table 4.
Guessed Alpha and Beta Energy Values
|
E(pi-)(MeV) |
E(p)(MeV) |
E(pi-)+E(p)(MeV) |
|
361.2 |
1318.7 |
1679.9 |
Percentage
Difference
Conclusion
by Bill Chun Wai Hung:
In this
experiment, we want to determine the identities of alpha and beta particles.
Since the
centripetal force in this experiment is
Since in this bubble chamber case, the force is also a
magnetic force, so
Reduce the equation gives
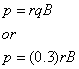
where r
is in centimeters, B in kilogauss=30.0kG(kilogauss) in this case, and p in
MeV/c.
By measuring the diagram, r
can be calculated by the following equation
So the momentum and energy of the pion, alpha, and beta particle can be calculated by the following equations.
The experimental values of the momentum and energies of
pion, alpha, and beta particles are
|
Elements |
h (cm) |
l (cm) |
r (cm) |
mv (MeV/c) |
E(MeV) |
|
Pi- |
5.7 |
30.6 |
84.9868421 |
764.881579 |
777.588471 |
|
Alpha |
5 |
31.7 |
102.989 |
926.901 |
(Table 2) |
|
Beta |
4.4 |
17.5 |
37.0011364 |
333.010227 |
(Table 2) |
The
percentage errors of the momentum are
|
Elements |
Target mv (MeV/c) |
Experimental mv (MeV/c) |
% Difference |
|
Pi- |
900 |
764.881579 |
15.013158 |
|
Alpha |
1089 |
926.901 |
14.885124 |
|
Beta |
387 |
333.010227 |
13.950846 |
Since
and 
can be calculated by the equation
The
results are
|
E(pi-)(MeV) |
E(p)(MeV) |
E(pi-)+E(p)(MeV) |
|
777.588471 |
938 |
1715.588471 |
Therefore, 
should equals to 1715.6MeV
From
the graph, the alpha particle bents left, while the beta particle bents right.
So alpha might be positive particles like proton(p),
pion positive(pi+), or Kaon positive (k+), while beta might be negative
particles like pion negative (pi-) or Kaon negative (k-).
The
table of possible alpha and beta particles is
|
Elements |
Rest
Energy (MeV) |
Total
Energy(MeV) |
|
p |
938 |
1318.7 |
|
pi+ |
140 |
937.4 |
|
k+ |
450 |
1030.4 |
|
pi- |
140 |
361.2 |
|
k- |
450 |
559.8 |
The
total energy of should equals to
1715.6MeV, so alpha particle is likely to be a proton, and beta particle is
likely to be a pion negative.
Calculating
by the equation , we have
|
E(alpha)(MeV) |
E(beta)(MeV) |
E(alpha)+E(beta)(MeV) |
|
361.2 |
1318.7 |
1679.9 |
1715.6MeV
is supposed to be equal to 1679.9MeV (the total energy of our guess)
calculated, but this is the best guess with the data obtained. The values are
off because of the errors discussed below. The percentage error for this energy
calculation is 2.08%
Error Analysis
The values are off because of
the measurement of the curving path of the particle are off by about +-1cm.
That is off by the measurement of l, h, and r.
The values are off also
because the value of momentum we used are only accurate to 3 or 4 significant
digits, that gives us an error in the calculation of the energy